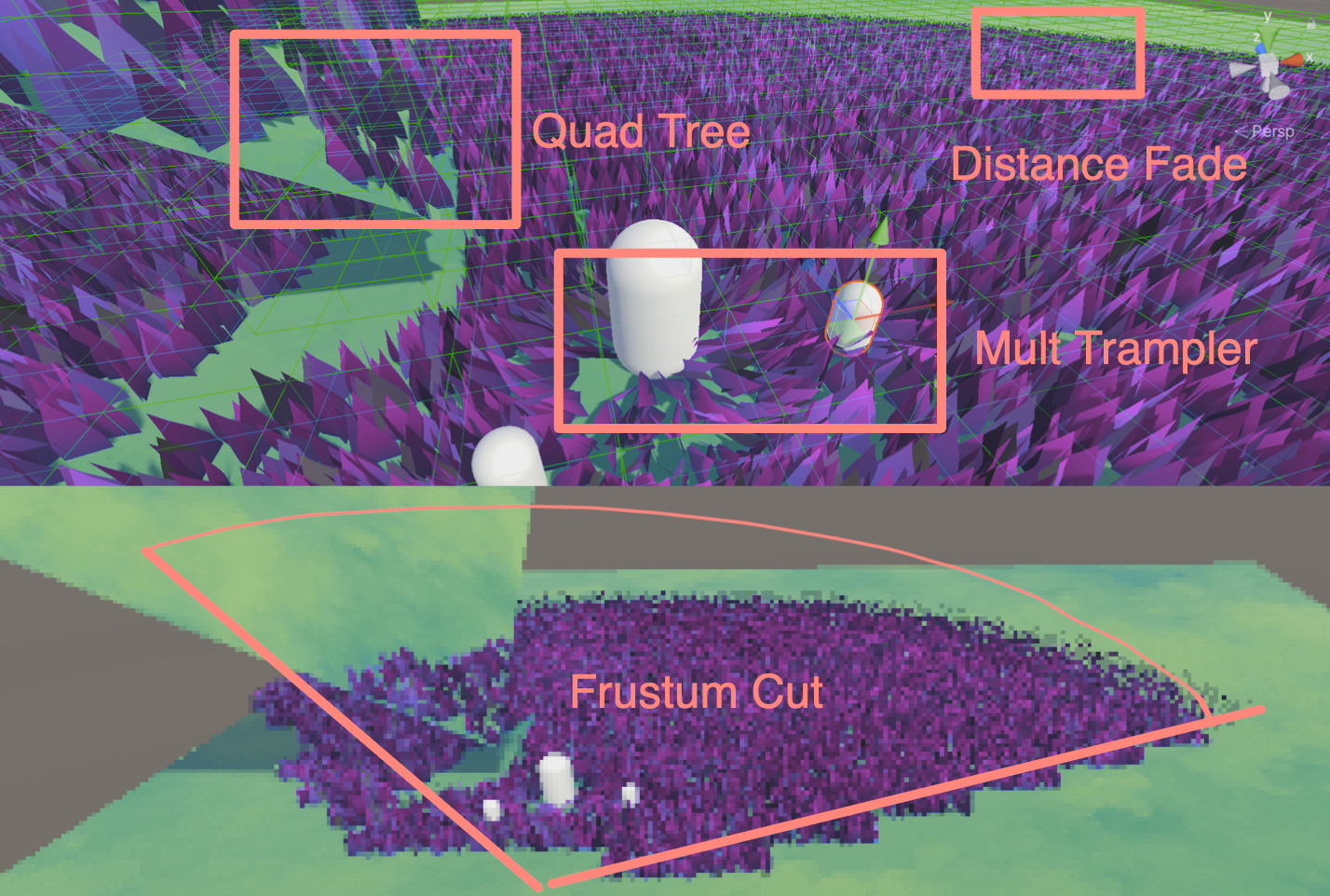
Tags: Getting Started/Shader/Tessellation Shader/Displacement Map/LOD/Smooth Outline/Early Culling
The word tessellation refers to a broad category of design activities, usually involving the arrangement of tiles of various geometric shapes next to each other to form a pattern on a flat surface. Its purpose can be artistic or practical, and many examples date back thousands of years. — Tessellation, Wikipedia, accessed July 2020.
This article mainly refers to:
Surface subdivision in game development is generally done in a triangleflat(or Quad) and then use the Displacement map to do vertex displacement, or use the Phong subdivision or PN triangles subdivision implemented in this article to do vertex displacement.
Phong subdivision does not need to know the adjacent topological information, only uses interpolation calculation, which is more efficient than PN triangles and other algorithms. Loop and Schaefer mentioned in GAMES101 use low-degree quadrilateral surfaces to approximate Catmull-Clark surfaces. The polygons input by these methods are replaced by a polynomial surface. The Phong subdivision in this article does not require any operation to correct additional geometric areas.
1. Overview of the tessellation process
This chapter introduces the process of surface subdivision in the rendering pipeline.
The tessellation shader is located after the vertex shader, and the tessellation is divided into three steps: Hull, Tesselllator and Domain, among which Tessellator is not programmable.

The first step of tessellation is the tessellation control shader (also known as Tessellation Control Shader, TCS), which will output control points and tessellation factors. This stage mainly consists of two parallel functions: Hull Function and Patch Constant Function.

Both functions receive patches, which are a set of vertex indices. For example, a triangle uses three numbers to represent the vertex indices. One patch can form a fragment, for example, a triangle fragment is composed of three vertex indices.
Moreover, the Hull Function is executed once for each vertex, and the Path Constant Function is executed once for each Patch. The former outputs the modified control point data (usually including vertex position, possible normals, texture coordinates and other attributes), while the latter outputs the constant data related to the entire fragment, that is, the subdivision factor. The subdivision factor tells the next stage (the tessellator) how to subdivide each fragment.
In general, the Hull Function modifies each control point, while the Patch Constant Function determines the level of subdivision based on the distance from the camera.

Next comes the non-programmable stage, the tessellator. It receives the patch and the subdivision factor just obtained. The tessellator generates a barycentric coordinate for each vertex data.

Next comes the last step, the Domain Stage (also known as Tessellation Evaluation Shader, TES), which is programmable. This part consists of domain functions, which are executed once per vertex. It receives the barycentric coordinates and the results generated by the two functions in the Patch and Hull Stage. Most of the logic is written here. The most important thing is that you can reposition the vertices in this stage, which is the most important part of tessellation.

If there is a geometry shader, it will be executed after the Domain Stage. But if not, it will come to the rasterization stage.

In summary, the first thing is the vertex shader. The Hull stage accepts vertex data and decides how to subdivide the mesh. Then the tessellator stage processes the subdivided mesh, and finally the Domain stage outputs vertices for the fragment shader.
2. Surface subdivision analysis
This chapter contains code analysis of Unity's surface subdivision, practical example effects display and an overview of the underlying principles.
2.1 Key code analysis
2.1.1 Basic settings of Unity tessellation
First of all, the tessellation shader needs to use shader target 5.0.
HLSLPROGRAM
#Pragmas target 5.0 // 5.0 required for tessellation
#Pragmas vertex Vertex
#Pragmas hull Hull
#Pragmas domain Domain
#Pragmas fragment Fragment
ENDHLSL2.1.2 Hull Stage Code 1 – Hull Function
In the classic process, the vertex shader converts the position and normal information into world space. Then the output result is passed to the Hull Stage. It should be noted that, unlike the vertex shader, the vertices of the Hull shader are represented by INTERNALTESSPOS semantics instead of POSITION semantics. The reason is that Hull does not need to output these vertex positions to the next rendering process, but for its own internal tessellation algorithm, so it will convert these vertices to a coordinate system that is more suitable for tessellation. In addition, developers can also distinguish more clearly.
struct Attributes {
float3 positionOS : POSITION;
float3 normalOS : NORMAL;
UNITY_VERTEX_INPUT_INSTANCE_ID
};
struct TessellationControlPoint {
float3 positionWS : INTERNAL LTESS POS;
float3 normalWS : NORMAL;
UNITY_VERTEX_INPUT_INSTANCE_ID
};
TessellationControlPoint Vertex(Attributes input) {
TessellationControlPoint output;
UNITY_SETUP_INSTANCE_ID(input);
UNITY_TRANSFER_INSTANCE_ID(input, output);
VertexPositionInputs posnInputs = GetVertexPositionInputs(input.positionOS);
VertexNormalInputs normalInputs = GetVertexNormalInputs(input.normalOS);
output.positionWS = posnInputs.positionWS;
output.normalWS = normalInputs.normalWS;
return output;
}Below are some setting parameters for the Hull Shader.
The first line, domain, defines the domain type of the tessellation shader, which means that both the input and output are triangle primitives. You can choose tri (triangle), quad (quadrilateral), etc.
The second line outputcontrolpoints indicates the number of output control points, 3 corresponds to the three vertices of the triangle.
The third line outputtopology indicates the topological structure of the primitive after subdivision. triangle_cw means that the vertices of the output triangle are sorted clockwise. The correct order can ensure that the surface faces outward. triangle_cw (clockwise around the triangle), triangle_ccw (counterclockwise around the triangle), line (line segment)
The fourth line patchconstantfunc is another function of the Hull Stage, which outputs constant data such as subdivision factors. A patch is executed only once.
The fifth line, partitioning, specifies how to distribute additional vertices to the edges of the original Path primitive. This step can make the subdivision process smoother and more uniform. integer, fractional_even, fractional_odd.
The maxtessfactor in the sixth line represents the maximum subdivision factor. Limiting the maximum subdivision can control the rendering burden.
[domain("tri")]
[outputcontrolpoints(3)]
[outputtopology("triangle_cw")]
[patchconstantfunc("patchconstant")]
[partitioning("fractional_even")]
[maxtessfactor(64.0)]In the Hull Shader, each control point will be called once independently, so this function will be executed the same number of control points. To know which vertex is currently being processed, we use the variable id with the semantics of SV_OutputControlPointID to determine. The function also passes in a special structure that can be used to easily access any control point in the Patch like an array.
TessellationControlPoint Hull(
InputPatch<TessellationControlPoint, 3> patch, uint id : SV_OutputControlPointID) {
TessellationControlPoint h;
// Hull shader code here
return patch[id];
}2.1.3 Hull Stage Code 2 – Patch Constant Function
In addition to the Hull Shader, there is another function in the Hull Stage that runs in parallel, the patch constant function. The signature of this function is relatively simple. It inputs a patch and outputs the calculated subdivision factor. The output structure contains the tessellation factor specified for each edge of the triangle. These factors are identified by the special system value semantics SV_TessFactor. Each tessellation factor defines how many small segments the corresponding edge should be subdivided into, thereby affecting the density and details of the resulting mesh. Let's take a closer look at what this factor specifically contains.
struct TessellationFactors {
float edge[3] : SV_TessFactor;
float inside : SV_InsideTessFactor;
};
// The patch constant function runs once per triangle, or "patch"
// It runs in parallel to the hull function
TessellationFactors PatchConstantFunction(
InputPatch<TessellationControlPoint, 3> patch) {
UNITY_SETUP_INSTANCE_ID(patch[0]); // Set up instancing
//Calculate tessellation factors
TessellationFactors f;
f.edge[0] = _FactorEdge1.x;
f.edge[1] = _FactorEdge1.y;
f.edge[2] = _FactorEdge1.z;
f.inside = _FactorInside;
return f;
}First, there is an edge tessellation factor edge[3] in the TessellationFactors structure, marked as SV_TessFactor. When using triangles as the basic primitives for tessellation, each edge is defined as being located relative to the vertex with the same index. Specifically: edge 0 corresponds to vertex 1 and vertex 2. Edge 1 corresponds to vertex 2 and vertex 0. Edge 2 corresponds to vertex 0 and vertex 1. Why is this so? The intuitive explanation is that the index of the edge is the same as the index of the vertex it is not connected to. This helps to quickly identify and process the edges corresponding to specific vertices when writing shader code.
There is also a center tessellation factor inside labeled SV_InsideTessFactor. This factor directly changes the final tessellation pattern, and more essentially determines the number of edge subdivisions, which is used to control the subdivision density inside the triangle. Compared with the edge subdivision factor, the center tessellation factor controls how the inside of the triangle is further subdivided into smaller triangles, while the edge tessellation factor affects the number of edge subdivisions.
Patch Constant Function can also output other useful data, but it must be labeled with the correct semantics. For example, BEZIERPOS semantics is very useful and can represent float3 data. This semantics will be used later to output the control points of the smoothing algorithm based on the Bezier curve.
2.1.4 Domain Stage Code
Next, we enter the Domain Stage. The Domain Function also has a Domain property, which should be the same as the output topology type of the Hull Function. In this example, it is set to a triangle. This function inputs the patch from the Hull Function, the output of the Patch Constant Function, and the most important vertex barycentric coordinates. The output structure is very similar to the output structure of the vertex shader, containing the position of the Clip space, as well as the lighting data required by the fragment shader.
It doesn’t matter if you don’t know what it is for now. Just read Chapter 4 of this article and then come back to study it.
Simply put, each new vertex that is subdivided will run this domain function.
struct Interpolators {
float3 normalWS : TEXCOORD0;
float3 positionWS : TEXCOORD1;
float4 positionCS : SV_POSITION;
};
// Call this macro to interpolate between a triangle patch, passing the field name
#define BARYCENTRIC_INTERPOLATE(fieldName) \
patch[0].fieldName * barycentricCoordinates.x + \
patch[1].fieldName * barycentricCoordinates.y + \
patch[2].fieldName * barycentricCoordinates.z
// The domain function runs once per vertex in the final, tessellated mesh
// Use it to reposition vertices and prepare for the fragment stage
[domain("tri")] // Signal we're inputting triangles
Interpolators Domain(
TessellationFactors factors, //The output of the patch constant function
OutputPatch<TessellationControlPoint, 3> patch, // The Input triangle
float3 barycentricCoordinates : SV_DomainLocation) { // The barycentric coordinates of the vertex on the triangle
Interpolators output;
// Setup instancing and stereo support (for VR)
UNITY_SETUP_INSTANCE_ID(patch[0]);
UNITY_TRANSFER_INSTANCE_ID(patch[0], output);
UNITY_INITIALIZE_VERTEX_OUTPUT_STEREO(output);
float3 positionWS = BARYCENTRIC_INTERPOLATE(positionWS);
float3 normalWS = BARYCENTRIC_INTERPOLATE(normalWS);
output.positionCS = TransformWorldToHClip(positionWS);
output.normalWS = normalWS;
output.positionWS = positionWS;
return output;
}In this function, Unity will give us the subdivision factor, the three vertices of the patch, and the centroid coordinates of the current new vertex. We can use this data to do displacement processing, etc.
2.2 Detailed explanation of subdivision factors and division modes
From thisLink Copy the code, then make the corresponding material and turn on the wireframe mode. We have only drawn vertices for the Mesh and have not applied any operations in the fragment shader, so it looks transparent.

If any component of the Edge Factor is set to 0 or less than 0, the Mesh will disappear completely. The following figure shows what it looks like after it disappears (the Unity editor's object border stroke is turned on). This feature is very important.

2.2.1 Overview of subdivision factors
To put it bluntly, after these factors are set in the Hull Stage, they are simply and crudely written into the barycentric coordinates in the Tessellation Stage, such as edge factors and internal factors. (Assuming they are all tri, if it is quad, it is calculated using uv, which may be more complicated, I don't know) This simple and crude stage is not programmable.

Take "integer (uniform) cutting mode" as an example. (temporarily) [partitioning("integer")] The domain is all triangles [domain("tri")] The number of output vertices is also 3. [outputcontrolpoints(3)] And the output topology is a triangle clockwise. [outputtopology("triangle_cw")]
2.2.2 Preparatory work and potential parallel issues
Modify the code to the following:
// .shader
_FactorEdge1("[Float3]Edge factors,[Float]Inside factor", Vector) = (1, 1, 1, 1) // -- Edited --
// .hlsl
float4 _FactorEdge1; // -- Edited --
...
f.edge[0] = _FactorEdge1.x;
f.edge[1] = _FactorEdge1.y; // -- Edited --
f.edge[2] = _FactorEdge1.z; // -- Edited --
f.inside = _FactorEdge1.w; // -- Edited --
There may be a problem here. Sometimes the compiler will split the Patch Constant Function and calculate each factor in parallel, which may cause some factors to be deleted, and the factors may be inexplicably equal to 0. The solution is to pack these factors into a vector so that the compiler will not use undefined quantities. The following is a simple reproduction of what may happen.
Modify the Path Constant Function as follows and open two new properties in the panel.
The modified code lines are commented out with // — Edited — .
// The patch constant function runs once per triangle, or "patch"
// It runs in parallel to the hull function
TessellationFactors PatchConstantFunction(
InputPatch<TessellationControlPoint, 3> patch) {
UNITY_SETUP_INSTANCE_ID(patch[0]); // Set up instancing
//Calculate tessellation factors
TessellationFactors f;
f.edge[0] = _FactorEdge1.x;
f.edge[1] = _FactorEdge2; // -- Edited --
f.edge[2] = _FactorEdge3; // -- Edited --
f.inside = _FactorInside;
return f;
}
_FactorEdge2("Edge 2 factor", Float) = 1 // -- Edited --
_FactorEdge3("Edge 3 factor", Float) = 1 // -- Edited --2.2.3 Edge Factor – SV_TessFactor
It can be seen that the edge factors correspond approximately to the number of times the corresponding edge is split, and the internal factor corresponds to the complexity of the center.
The edge factor only affectsOriginal triangle edgeAs for the complex internal pattern, it is controlled by the internal factor Inside Factor and the division mode.
It should be noted that the surface subdivision in "integer cutting mode" is rounded up, for example, 2.1 is rounded up to 3.

One picture says it all.

2.2.4 Inside Factor – SV_InsideTessFactor
Let's take the INTEGER mode as an example. The internal factor will only affect the complexity of the internal pattern. The specific influence is described in detail below.To summarize, the edge factor affects the triangular subdivision between the outermost layer and the first layer, the internal factor affects how many layers there are, and the division mode affects how each internal layer is subdivided.
Assuming that the Edge Factors are set to (2,3,4) and only the Insider Factor is modified, an interesting property can be observed: when the internal factor n is an even number, a vertex can be found whose coordinates are exactly at the centroid position (13,13,13).
Generally, it is good to set the edge factors to the same value. Here, different values are set, and the graph may be more confusing, but the most essential rules can be seen.

It can be further observed that the number of vertices on any edge closest to the outermost triangle has an equal relationship with the internal factor Inside Factor (n): n=Numpoint−1. That is, the number of vertices on this edge is always equal to the subdivision factor minus 1.

The number of vertices in each layer decreases by 1. That is, the first layer (not counting the outermost layer, as it will not be subdivided) will have n vertices, the second layer inward will have n−2 vertices, and so on.
Combining the above three observations, we can get a guess and conclusion(It’s useless, but I calculated it when I had nothing to do)The total number of internal vertices can be calculated using the formula, where n corresponds to the internal factor n-1. Note that the internal factor starts at 2: a2n=3n2a2n−1=3n(n−1)+1. This can be simplified and combined to: ak=−0.125(−1)k+0.75k2+0.125. The formula for all integer operations is as follows: ak=⌊−(−1)k+6k2+18⌋

2.2.5 Partitioning Mode – [partitioning(“_”)]
The above only describes the simplest way to divide integers evenly, which uses integer multiples for subdivision. Let's talk about the other methods.Simply put, Fractional Odd and Fractional Even are advanced versions of Integer, but the former is an advanced version of Integer when it is an odd number, and the latter is an advanced version of Integer when it is an even number. The specific advancement is that the fractional part can be used to make the division no longer equal.

Fractional Odd: Inside Factor can be a fraction (not Ceil), and the denominator is an odd number. Note that the denominator here is actually the denominator represented by the barycentric coordinates of each vertex. The division method with an odd number as the denominator will definitely make a vertex fall on the barycentric coordinates of the triangle, while an even number will not.Kaios.

Fractional Even: Similar to fractional_odd, but with an even denominator. I'm not sure how to choose this.

Pow2 (power of 2): This mode only allows the use of powers of 2 (such as 1, 2, 4, 8, etc.) as subdivision levels. Generally used for texture mapping or shadow calculations.
3. Segment Optimization
3.1 View Frustum Culling
Generating so many vertices will result in very bad performance! Therefore, some methods are needed to improve rendering efficiency. Although vertices outside the frustum will be culled before T rasterization, if unnecessary patches are culled in advance in TCS, the calculation pressure of the tessellation shader will be reduced.
If the tessellation factor is set to 0 in the Patch Constant Function, the tessellation generator will ignore the patch, which means that the culling here is for the entire patch, rather than the vertex-by-vertex culling in the frustum culling.
We test every point in the patch to see if they are out of view. To do this, transform every point in the patch into clip space. So we need to calculate the clip space coordinates of each point in the vertex shader and pass it to the Hull Stage. Use GetVertexPositionInputs to get what we want.
struct TessellationControlPoint {
float4 positionCS : SV_POSITION; // -- Edited --
...
};
TessellationControlPoint Vertex(Attributes input) {
TessellationControlPoint output;
...
VertexPositionInputs posnInputs = GetVertexPositionInputs(input.positionOS);
...
output.positionCS = posnInputs.positionCS; // -- Edited --
...
return output;
}Then write a test function above the Patch Constant Function to determine whether to cull the patch. Temporarily pass false here. The function passes in three points in the clipping space.
// Returns true if it should be clipped due to frustum or winding culling
bool ShouldClipPatch(float4 p0PositionCS, float4 p1PositionCS, float4 p2PositionCS) {
return false;
}Then write the IsOutOfBounds function to test whether a point is outside the bounds. The bounds can also be specified, and this method can be used in another function to determine whether a point is outside the view frustum.
// Returns true if the point is outside the bounds set by lower and higher
bool IsOutOfBounds(float3 p, float3 lower, float3 higher) {
return p.x < lower.x || p.x > higher.x || p.y < lower.y || p.y > higher.y || p.z < lower.z || p.z > higher.z;
}
// Returns true if the given vertex is outside the camera fustum and should be culled
bool IsPointOutOfFrustum(float4 positionCS) {
float3 culling = positionCS.xyz;
float w = positionCS.w;
// UNITY_RAW_FAR_CLIP_VALUE is either 0 or 1, depending on graphics API
// Most use 0, however OpenGL uses 1
float3 lowerBounds = float3(-w, -w, -w * UNITY_RAW_FAR_CLIP_VALUE);
float3 higherBounds = float3(w, w, w);
return IsOutOfBounds(culling, lowerBounds, higherBounds);
}In Clip Space, the W component is the secondary coordinate that determines whether a point is in the view frustum. If xyz is outside the range [-w, w], these points will be culled because they are outside the view frustum. Different APIs have differentDepth of processingThere is a different logic on the , we need to pay attention when we use this component as the boundary. DirectX and Vulkan use the left-handed system, the Clip depth is [0, 1], so UNITY_RAW_FAR_CLIP_VALUE is 0. OpenGL is a right-handed system, the Clip depth range is [-1, 1], and UNITY_RAW_FAR_CLIP_VALUE is 1.
After preparing these, you can determine whether a patch needs to be culled. Go back to the function at the beginning and determine whether all the points of a patch need to be culled.
// Returns true if it should be clipped due to frustum or winding culling
bool ShouldClipPatch(float4 p0PositionCS, float4 p1PositionCS, float4 p2PositionCS) {
bool allOutside = IsPointOutOfFrustum(p0PositionCS) &&
IsPointOutOfFrustum(p1PositionCS) &&
IsPointOutOfFrustum(p2PositionCS); // -- Edited --
return allOutside; // -- Edited --
}3.2 Backface Culling
In addition to frustum culling, patches can also undergo backface culling, using the normal vector to determine whether a patch needs to be culled.

The normal vector is obtained by taking the cross product of two vectors. Since we are currently in Clip space, we need to do a perspective division to get NDC, which should be in the range of [-1,1]. The reason for converting to NDC is that the position in Clip space is nonlinear, which may cause the position of the vertex to be distorted. Converting to a linear space like NDC can more accurately determine the front and back relationship of the vertices.
// Returns true if the points in this triangle are wound counter-clockwise
bool ShouldBackFaceCull(float4 p0PositionCS, float4 p1PositionCS, float4 p2PositionCS) {
float3 point0 = p0PositionCS.xyz / p0PositionCS.w;
float3 point1 = p1PositionCS.xyz / p1PositionCS.w;
float3 point2 = p2PositionCS.xyz / p2PositionCS.w;
float3 normal = cross(point1 - point0, point2 - point0);
return dot(normal, float3(0, 0, 1)) < 0;
}The above code still has a cross-platform problem. The viewing direction is different in different APIs, so modify the code.
// In clip space, the view direction is float3(0, 0, 1), so we can just test the z coord
#if UNITY_REVERSED_Z
return cross(point1 - point0, point2 - point0).z < 0;
#else // In OpenGL, the test is reversed
return cross(point1 - point0, point2 - point0).z > 0;
#endifFinally, add the function you just wrote to ShouldClipPatch to determine backface culling.
// Returns true if it should be clipped due to frustum or winding culling
bool ShouldClipPatch(float4 p0PositionCS, float4 p1PositionCS, float4 p2PositionCS) {
bool allOutside = IsPointOutOfFrustum(p0PositionCS) &&
IsPointOutOfFrustum(p1PositionCS) &&
IsPointOutOfFrustum(p2PositionCS);
return allOutside || ShouldBackFaceCull(p0PositionCS, p1PositionCS, p2PositionCS); // -- Edited --
}Then set the vertex factor of the patch to be culled to 0 in PatchConstantFunction.
...
if (ShouldClipPatch(patch[0].positionCS, patch[1].positionCS, patch[2].positionCS)) {
f.edge[0] = f.edge[1] = f.edge[2] = f.inside = 0; // Cull the patch
}
...3.3 Increase Tolerance
You may want to verify the correctness of the code, or there may be some unexpected exclusions. In this case, adding a tolerance is a flexible approach.
The first is the frustum culling tolerance. If the tolerance is positive, the culling boundaries will be expanded so that some objects near the edge of the frustum will not be culled even if they are partially out of bounds. This method can reduce the frequent changes in culling state due to small perspective changes or object dynamics.
// Returns true if the given vertex is outside the camera fustum and should be culled
bool IsPointOutOfFrustum(float4 positionCS, float tolerance) {
float3 culling = positionCS.xyz;
float w = positionCS.w;
// UNITY_RAW_FAR_CLIP_VALUE is either 0 or 1, depending on graphics API
// Most use 0, however OpenGL uses 1
float3 lowerBounds = float3(-w - tolerance, -w - tolerance, -w * UNITY_RAW_FAR_CLIP_VALUE - tolerance);
float3 higherBounds = float3(w + tolerance, w + tolerance, w + tolerance);
return IsOutOfBounds(culling, lowerBounds, higherBounds);
}Next, backface culling is adjusted. In practice, this is done by comparing to a tolerance instead of zero to avoid issues with numerical precision. If the dot product result is less than some small positive value (the tolerance) instead of being strictly less than zero, then the primitive is considered a backface. This approach provides an additional buffer, ensuring that only explicitly backface primitives are culled.
// Returns true if the points in this triangle are wound counter-clockwise
bool ShouldBackFaceCull(float4 p0PositionCS, float4 p1PositionCS, float4 p2PositionCS, float tolerance) {
float3 point0 = p0PositionCS.xyz / p0PositionCS.w;
float3 point1 = p1PositionCS.xyz / p1PositionCS.w;
float3 point2 = p2PositionCS.xyz / p2PositionCS.w;
// In clip space, the view direction is float3(0, 0, 1), so we can just test the z coord
#if UNITY_REVERSED_Z
return cross(point1 - point0, point2 - point0).z < -tolerance;
#else // In OpenGL, the test is reversed
return cross(point1 - point0, point2 - point0).z > tolerance;
#endif
}It is possible to expose a Range in the Material Panel.
// .shader
Properties{
_tolerance("_tolerance",Range(-0.002,0.001)) = 0
...
}
// .hlsl
float _tolerance;
...
// Returns true if it should be clipped due to frustum or winding culling
bool ShouldClipPatch(float4 p0PositionCS, float4 p1PositionCS, float4 p2PositionCS) {
bool allOutside = IsPointOutOfFrustum(p0PositionCS, _tolerance) &&
IsPointOutOfFrustum(p1PositionCS, _tolerance) &&
IsPointOutOfFrustum(p2PositionCS, _tolerance); // -- Edited --
return allOutside || ShouldBackFaceCull(p0PositionCS, p1PositionCS, p2PositionCS,_tolerance); // -- Edited --
}
3.4 Dynamic subdivision factor
So far, our algorithm has subdivided all surfaces indiscriminately. However, in a complex Mesh, there may be large and small faces.Uneven Mesh AreaThe large face is more obvious visually due to its large area, and more subdivisions are needed to ensure the smoothness and details of the surface. The small face is small in area, so you can consider reducing the subdivision level of this part, which will not have a big impact on the visual effect. Dynamically changing the factor according to the length change is a common method. Set an algorithm to give faces with longer side lengths a higher subdivision factor.
In addition to the large and small faces of the Mesh itself,The distance between the camera and the patchIt can also be used as a factor to dynamically change the factor. Objects that are farther away from the camera can have a lower tessellation factor because they occupy fewer pixels on the screen.The user’s viewing angle and gaze direction, you can prioritize subdividing faces that face the camera, and reduce the level of subdivision for faces that face away from the camera or to the sides.
3.4.1 Fixed Segment Scaling
Get the distance between two vertices. The larger the distance, the larger the subdivision factor. The scale is exposed in the control panel and set to [0,1]. When the scale is 1, the subdivision factor is directly contributed by the distance between the two points. The closer the scale is to 0, the larger the subdivision factor. In addition, an initial value bias is added. Finally, let it take a number of 1 or above to ensure accuracy.
//Calculate the tessellation factor for an edge
float EdgeTessellationFactor(float scale, float bias, float3 p0PositionWS, float3 p1PositionWS) {
float factor = distance(p0PositionWS, p1PositionWS) / scale;
return max(1, factor + bias);
}Then modify the material panel and Patch Constant Function. Generally speaking, the average value of the edge subdivision factor is used as the internal subdivision factor, which will give a more consistent visual effect.
// .shader
Properties{
...
_TessellationBias("_TessellationBias", Range(-1,5)) = 1
_TessellationFactor("_TessellationFactor", Range(0,1)) = 0
}
// .hlsl
f.edge[0] = EdgeTessellationFactor(_TessellationFactor, _TessellationBias, patch[1].positionWS, patch[2].positionWS);
f.edge[1] = EdgeTessellationFactor(_TessellationFactor, _TessellationBias, patch[2].positionWS, patch[0].positionWS);
f.edge[2] = EdgeTessellationFactor(_TessellationFactor, _TessellationBias, patch[0].positionWS, patch[1].positionWS);
f.inside = (f.edge[0] + f.edge[1] + f.edge[2]) / 3.0;The degree of subdivision of fragments of different sizes will change dynamically, and the effect is as follows.

By the way, if you find that your internal factor pattern is very strange, this may be caused by the compiler. Try to modify the internal factor code to the following to solve it.
f.inside = ( // If the compiler doesn't play nice...
EdgeTessellationFactor(_TessellationFactor, _TessellationBias, patch[1].positionWS, patch[2].positionWS) +
EdgeTessellationFactor(_TessellationFactor, _TessellationBias, patch[2].positionWS, patch[0].positionWS) +
EdgeTessellationFactor(_TessellationFactor, _TessellationBias, patch[0].positionWS, patch[1].positionWS)
) / 3.0;3.4.2 Screen Space Subdivision Scaling
Next, we need to determine the camera distance. We can directlyUse screen space distance to adjust the subdivision level, which perfectly solves the problem of large and small surfaces + screen distance at the same time!
Since we already have the data in Clip space, and since screen space is very similar to NDC space, we only need to convert it to NDC, that is, do a perspective division.
float EdgeTessellationFactor(float scale, float bias, float3 p0PositionWS, float4 p0PositionCS, float3 p1PositionWS, float4 p1PositionCS) {
float factor = distance(p0PositionCS.xyz / p0PositionCS.w, p1PositionCS.xyz / p1PositionCS.w) / scale;
return max(1, factor + bias);
}Next, pass the Clip space coordinates into the Patch Constant Function.
f.edge[0] = EdgeTessellationFactor(_TessellationFactor, _TessellationBias,
patch[1].positionWS, patch[1].positionCS, patch[2].positionWS, patch[2].positionCS);
f.edge[1] = EdgeTessellationFactor(_TessellationFactor, _TessellationBias,
patch[2].positionWS, patch[2].positionCS, patch[0].positionWS, patch[0].positionCS);
f.edge[2] = EdgeTessellationFactor(_TessellationFactor, _TessellationBias,
patch[0].positionWS, patch[0].positionCS, patch[1].positionWS, patch[1].positionCS);
f.inside = (f.edge[0] + f.edge[1] + f.edge[2]) / 3.0;The current effect is quite good, and the level of subdivision changes dynamically as the camera distance (screen space distance) changes. If you use a subdivision mode other than INTEGER, you will get a more consistent effect.

There are still some areas that can be improved. For example, the unit of the scaling factor. Just now we controlled it to [0,1], which is not very suitable for us to adjust. We multiply it by the screen resolution and change the scaling factor range to [0,1080], which is more convenient for us to adjust. Then modify the material panel properties. Now it is a ratio in pixels.
// .hlsl
float factor = distance(p0PositionCS.xyz / p0PositionCS.w, p1PositionCS.xyz / p1PositionCS.w) * _ScreenParams.y / scale;
// .shader
_TessellationFactor("_TessellationFactor",Range(0,1080)) = 320
3.4.3 Camera distance subdivision scaling
How do we use camera distance scaling? It's very simple. We calculate the ratio of the distance between two points and the distance between the midpoint of the two vertices and the camera position. The larger the ratio, the larger the space occupied on the screen, and the more subdivision is needed.
// .hlsl
float EdgeTessellationFactor(float scale, float bias, float3 p0PositionWS, float3 p1PositionWS) {
float length = distance(p0PositionWS, p1PositionWS);
float distanceToCamera = distance(GetCameraPositionWS(), (p0PositionWS + p1PositionWS) * 0.5);
float factor = length / (scale * distanceToCamera * distanceToCamera);
return max(1, factor + bias);
}
...
f.edge[0] = EdgeTessellationFactor(_TessellationFactor, _TessellationBias, patch[1].positionWS, patch[2].positionWS);
f.edge[1] = EdgeTessellationFactor(_TessellationFactor, _TessellationBias, patch[2].positionWS, patch[0].positionWS);
f.edge[2] = EdgeTessellationFactor(_TessellationFactor, _TessellationBias, patch[0].positionWS, patch[1].positionWS);
// .shader
_TessellationFactor("_TessellationFactor",Range(0, 1)) = 0.02Note that the scaling factor is no longer in pixels, but in the original [0,1] unit. Because screen pixels are not very meaningful in this method, they are not used. And the world coordinates are used again.
The results of screen space subdivision scaling and camera distance subdivision scaling are similar. Generally, a macro can be opened to switch the modes of the above dynamic factors. Here, it is left to the reader to complete.
3.5 Specifying subdivision factors
3.5.1 Vertex Storage Subdivision Factor
In the previous section, we used different strategies to guess the appropriate subdivision factors. If we know exactly how the mesh should be subdivided, we can store the coefficients of these subdivision factors in the mesh. Since the coefficient only needs a float, only one color channel is needed. The following is a pseudo code, just give it a try.
float EdgeTessellationFactor(float scale, float bias, float multiplier) {
...
return max(1, (factor + bias) * multiplier);
}
...
// PCF()
[unroll] for (int i = 0; i < 3; i++) {
multipliers[i] = patch[i].color.g;
}
//Calculate tessellation factors
f.edge[0] = EdgeTessellationFactor(_TessellationFactor, _TessellationBias, (multipliers[1] + multipliers[2]) / 2);
3.5.2 SDF Control Surface Subdivision Factor
It is quite cool to combine the Signed Distance Field (SDF) to control the tessellation factor. Of course, this section does not involve the generation of SDF, assuming that it can be directly obtained through the ready-made function CalculateSDFDistance.
For a given Mesh, use CalculateSDFDistance to calculate the distance from each vertex in each patch to the shape represented by the SDF (such as a sphere). After obtaining the distance, evaluate the subdivision requirements of the patch and perform subdivision.
TessellationFactors PatchConstantFunction(
InputPatch<TessellationControlPoint, 3> patch) {
float multipliers[3];
// Loop through each vertex
[unroll] for (int i = 0; i < 3; i++) {
// Calculate the distance from each vertex to the SDF surface
float sdfDistance = CalculateSDFDistance(patch[i].positionWS);
// Adjust subdivision factor based on SDF distance
if (sdfDistance < _TessellationDistanceThreshold) {
multipliers[i] = lerp(_MinTessellationFactor, _MaxTessellationFactor, (1 - sdfDistance / _TessellationDistanceThreshold));
} else {
multipliers[i] = _MinTessellationFactor;
}
}
// Calculate the final subdivision factor
TessellationFactors f;
f.Edge[0] = max(multipliers[0], multipliers[1]);
f.Edge[1] = max(multipliers[1], multipliers[2]);
f.Edge[2] = max(multipliers[2], multipliers[0]);
f.Inside = (multipliers[0] + multipliers[1] + multipliers[2]) / 3;
return f;
}I don't know how to implement it specifically, so I'll try to understand it first.

4. Vertex offset – contour smoothing
The easiest way to add details to a mesh is to use various high-resolution textures. However, the bottom line is that adding more vertices to a mesh is better than increasing the texture resolution. For example, a normal map can change the direction of each fragment's normal, but it does not change the geometry. Even a 128K texture cannot eliminate aliasing and pointy edges.

Therefore, we need to tessellate the surface and then offset the vertices. All the tessellation operations just mentioned are operated on the plane where the patch is located. If we want to bend these vertices, one of the simplest operations is Phong tessellation.
4.1 Phong subdivision
First, the original paper is attached. https://perso.telecom-paristech.fr/boubek/papers/PhongTessellation/PhongTessellation.pdf
Phong shading should be familiar to you. It is a technique that uses linear interpolation of normal vectors to obtain smooth shading. Phong subdivision is inspired by Phong shading and extends the concept of Phong shading to the spatial domain.
The core idea of Phong subdivision is to use the vertex normals of each corner of the triangle to affect the position of new vertices during the subdivision process, thereby creating a curved surface instead of a flat surface.
It is worth noting that many tutorials here use triangle corner to represent vertices. I think they are all the same, so I will still use vertices in this article.
First, in the Domain function, Unity will give us the centroid coordinates of the new vertex we need to process. Suppose we are currently processing (13,13,13).

Each vertex of a patch has a normal. Imagine a tangent plane emanating from each vertex, perpendicular to the respective normal vector.


Then project the current vertex onto these three tangent planes respectively.

Describe it in mathematical language. P′=P−((P−V)⋅N)N
in :
- $P$ is the initially interpolated plane position.
- $V$ is a vertex position on the plane.
- $N$ is the normal at vertex $V$.
- ⋅ represents the dot product.
- P′ is the projection of $P$ on the plane.
Get three $P'$.


The three points projected on the three tangent planes are re-formed into a new triangle, and then the centroid coordinates of the current vertex are applied to the new triangle to calculate the new point.

//Calculate Phong projection offset
float3 PhongProjectedPosition(float3 flatPositionWS, float3 cornerPositionWS, float3 normalWS) {
return flatPositionWS - dot(flatPositionWS - cornerPositionWS, normalWS) * normalWS;
}
// Apply Phong smoothing
float3 CalculatePhongPosition(float3 bary, float3 p0PositionWS, float3 p0NormalWS,
float3 p1PositionWS, float3 p1NormalWS, float3 p2PositionWS, float3 p2NormalWS) {
float3 smoothedPositionWS =
bary.x * PhongProjectedPosition(flatPositionWS, p0PositionWS, p0NormalWS) +
bary.y * PhongProjectedPosition(flatPositionWS, p1PositionWS, p1NormalWS) +
bary.z * PhongProjectedPosition(flatPositionWS, p2PositionWS, p2NormalWS);
return smoothedPositionWS;
}
// The domain function runs once per vertex in the final, tessellated mesh
// Use it to reposition vertices and prepare for the fragment stage
[domain("tri")] // Signal we're inputting triangles
Interpolators Domain(
TessellationFactors factors, //The output of the patch constant function
OutputPatch<TessellationControlPoint, 3> patch, // The Input triangle
float3 barycentricCoordinates : SV_DomainLocation) { // The barycentric coordinates of the vertex on the triangle
Interpolators output;
...
float3 positionWS = CalculatePhongPosition(barycentricCoordinates,
patch[0].positionWS, patch[0].normalWS,
patch[1].positionWS, patch[1].normalWS,
patch[2].positionWS, patch[2].normalWS);
float3 normalWS = BARYCENTRIC_INTERPOLATE(normalWS);
float3 tangentWS = BARYCENTRIC_INTERPOLATE(tangentWS.xyz);
...
output.positionCS = TransformWorldToHClip(positionWS);
output.normalWS = normalWS;
output.positionWS = positionWS;
output.tangentWS = float4(tangentWS, patch[0].tangentWS.w);
...
}Note that we need to add the normal vector here, and then write it into Vertex and Domain. Then write a function to calculate the coordinates of the center of gravity of $P'$.
struct Attributes {
...
float4 tangentOS : TANGENT;
};
struct TessellationControlPoint {
...
float4 tangentWS : TANGENT;
};
struct Interpolators {
...
float4 tangentWS : TANGENT;
};
TessellationControlPoint Vertex(Attributes input) {
TessellationControlPoint output;
...
// .....The last one is the symbol coefficient
output.tangentWS = float4(normalInputs.tangentWS, input.tangentOS.w); // tangent.w contains bitangent multiplier
}
// Barycentric interpolation as a function
float3 BarycentricInterpolate(float3 bary, float3 a, float3 b, float3 c) {
return bary.x * a + bary.y * b + bary.z * c;
}
In the original Phong subdivision paper, an α factor was added to control the degree of curvature. The original author recommends setting this value globally to three-quarters for the best visual effect. Expanding the algorithm with the α factor can produce a quadratic Bezier curve, which does not provide an inflection point but is sufficient for practical development.

First, let’s look at the formula in the original paper.

Essentially, it controls the degree of interpolation. A quantitative analysis shows that when α=0, all vertices are on the original plane, which is equivalent to no displacement. When α=1, the new vertices are completely dependent on the Phong subdivision bending vertices. Of course, you can also try values less than zero or greater than one, and the effect is also quite interesting. ~~It doesn’t matter if you don’t understand the mathematical formulas in the original text. I will just use a lerp and make a random interpolation.~~
// Apply Phong smoothing
float3 CalculatePhongPosition(float3 bary, float smoothing, float3 p0PositionWS, float3 p0NormalWS,
float3 p1PositionWS, float3 p1NormalWS, float3 p2PositionWS, float3 p2NormalWS) {
float3 flatPositionWS = BarycentricInterpolate(bary, p0PositionWS, p1PositionWS, p2PositionWS);
float3 smoothedPositionWS =
bary.x * PhongProjectedPosition(flatPositionWS, p0PositionWS, p0NormalWS) +
bary.y * PhongProjectedPosition(flatPositionWS, p1PositionWS, p1NormalWS) +
bary.z * PhongProjectedPosition(flatPositionWS, p2PositionWS, p2NormalWS);
return lerp(flatPositionWS, smoothedPositionWS, smoothing);
}
// Apply Phong smoothing
float3 CalculatePhongPosition(float3 bary, float smoothing, float3 p0PositionWS, float3 p0NormalWS,
float3 p1PositionWS, float3 p1NormalWS, float3 p2PositionWS, float3 p2NormalWS) {
float3 flatPositionWS = BarycentricInterpolate(bary, p0PositionWS, p1PositionWS, p2PositionWS);
float3 smoothedPositionWS =
bary.x * PhongProjectedPosition(flatPositionWS, p0PositionWS, p0NormalWS) +
bary.y * PhongProjectedPosition(flatPositionWS, p1PositionWS, p1NormalWS) +
bary.z * PhongProjectedPosition(flatPositionWS, p2PositionWS, p2NormalWS);
return lerp(flatPositionWS, smoothedPositionWS, smoothing);
}Don't forget to expose in the material panel.
// .shader
_TessellationSmoothing("_TessellationSmoothing", Range(0,1)) = 0.5
// .hlsl
float _TessellationSmoothing;
Interpolators Domain( .... ) {
...
float smoothing = _TessellationSmoothing;
float3 positionWS = CalculatePhongPosition(barycentricCoordinates, smoothing,
patch[0].positionWS, patch[0].normalWS,
patch[1].positionWS, patch[1].normalWS,
patch[2].positionWS, patch[2].normalWS);
...
}
It is important to note that some models require some modification. If the edges of the model are very sharp, it means that the normal of this vertex is almost parallel to the normal of the face. In Phong Tessellation, this will cause the projection of the vertex on the tangent plane to be very close to the original vertex position, thus reducing the impact of subdivision.
To solve this problem, you can add more geometric details by performing what is called "adding loop edges" or "loop cuts" in the modeling software. Insert additional edge loops near the edges of the original model to increase the subdivision density. The specific operation will not be expanded here.
In general, the effect and performance of Phong subdivision are relatively good. However, if you want a higher quality smoothing effect, you can consider PN triangles. This technology is based on the curved triangle of Bezier curve.
4.2 PN triangles subdivision
First, here is the original paper. http://alex.vlachos.com/graphics/CurvedPNTriangles.pdf
PN Triangles does not require information about neighboring triangles and is less expensive. The PN Triangles algorithm only requires the positions and normals of the three vertices in the patch. The rest of the data can be calculated. Note that all data is in barycentric coordinates.
In the PN algorithm, 10 control points need to be calculated for surface subdivision, as shown in the figure below. Three triangle vertices, a centroid, and three pairs of control points on the edges constitute all the control points. The calculated Bezier curve control points will be passed to the Domain. Since the control points of each triangle patch are consistent, it is very appropriate to place the step of calculating the control points in the Patch Constant Function.

The calculation method in the paper is as follows:
$$
\begin{aligned}
b_{300} & =P_1 \
b_{030} & =P_2 \
b_{003} & =P_3 \
w_{ij} & =\left(P_j-P_i\right) \cdot N_i \in \mathbf{R} \quad \text { here ' } \cdot \text { ' is the scalar product, } \
b_{210} & =\left(2 P_1+P_2-w_{12} N_1\right) / 3 \
b_{120} & =\left(2 P_2+P_1-w_{21} N_2\right) / 3 \
b_{021} & =\left(2 P_2+P_3-w_{23} N_2\right) / 3 \
b_{012} & =\left(2 P_3+P_2-w_{32} N_3\right) / 3 \
b_{102} & =\left(2 P_3+P_1-w_{31} N_3\right) / 3, \
b_{201} & =\left(2 P_1+P_3-w_{13} N_1\right) / 3, \
E & =\left(b_{210}+b_{120}+b_{021}+b_{012}+b_{102}+b_{201}\right) / 6 \
V & =\left(P_1+P_2+P_3\right) / 3, \
b_{111} & =E+(EV) / 2 .
\end{aligned}
$$
Each edge of the formula $w_{ij}$ is calculated twice, so a total of 6 times. For example, the meaning of $w_{1 2}$ is the projection length of the vector from $P_1$ to $P_2$ in the normal direction of $P_1$. Multiplying it by the corresponding normal direction means that the projection vector is $w$ in length.
Let's take the calculation of the factor close to $P_1$ as an example. The weight of the current position point should be larger. Multiplying it by $2$ makes the calculated control point closer to the current vertex. The reason for subtracting the projection vector is to correct the error caused by the position of $P_2$ not being on the plane defined by the $P_1$ normal. Make the triangle plane more consistent and reduce the distortion effect. Finally, divide by 3 for standardization.
Next, calculate the average Bezier control point $E$, which represents the average position of the six control points. This average position represents the concentration trend of the boundary control points. Then calculate the average position of the triangle vertices. Then find the midpoint of these two average positions and add it to the Bezier average control point. This is the tenth parameter required in the end.
To summarize, the first three are the positions of the triangle vertices (so they don't need to be written in the structure), six are calculated by weight, and the last one is the average of the previous calculations. The code is very simple to write.
struct TessellationFactors {
float edge[3] : SV_TessFactor;
float inside : SV_InsideTessFactor;
float3 bezierPoints[7] : BEZIERPOS;
};
//Bezier control point calculations
float3 CalculateBezierControlPoint(float3 p0PositionWS, float3 aNormalWS, float3 p1PositionWS, float3 bNormalWS) {
float w = dot(p1PositionWS - p0PositionWS, aNormalWS);
return (p0PositionWS * 2 + p1PositionWS - w * aNormalWS) / 3.0;
}
void CalculateBezierControlPoints(inout float3 bezierPoints[7],
float3 p0PositionWS, float3 p0NormalWS, float3 p1PositionWS, float3 p1NormalWS, float3 p2PositionWS, float3 p2NormalWS) {
bezierPoints[0] = CalculateBezierControlPoint(p0PositionWS, p0NormalWS, p1PositionWS, p1NormalWS);
bezierPoints[1] = CalculateBezierControlPoint(p1PositionWS, p1NormalWS, p0PositionWS, p0NormalWS);
bezierPoints[2] = CalculateBezierControlPoint(p1PositionWS, p1NormalWS, p2PositionWS, p2NormalWS);
bezierPoints[3] = CalculateBezierControlPoint(p2PositionWS, p2NormalWS, p1PositionWS, p1NormalWS);
bezierPoints[4] = CalculateBezierControlPoint(p2PositionWS, p2NormalWS, p0PositionWS, p0NormalWS);
bezierPoints[5] = CalculateBezierControlPoint(p0PositionWS, p0NormalWS, p2PositionWS, p2NormalWS);
float3 avgBezier = 0;
[unroll] for (int i = 0; i < 6; i++) {
avgBezier += bezierPoints[i];
}
avgBezier /= 6.0;
float3 avgControl = (p0PositionWS + p1PositionWS + p2PositionWS) / 3.0;
bezierPoints[6] = avgBezier + (avgBezier - avgControl) / 2.0;
}
// The patch constant function runs once per triangle, or "patch"
// It runs in parallel to the hull function
TessellationFactors PatchConstantFunction(
InputPatch<TessellationControlPoint, 3> patch) {
...
TessellationFactors f = (TessellationFactors)0;
// Check if this patch should be culled (it is out of view)
if (ShouldClipPatch(...)) {
...
} else {
...
CalculateBezierControlPoints(f.bezierPoints, patch[0].positionWS, patch[0].normalWS,
patch[1].positionWS, patch[1].normalWS, patch[2].positionWS, patch[2].normalWS);
}
return f;
}Then, in the domain function, use the ten factors output by the Hull Function. According to the formula given in the paper, calculate the final cubic Bezier surface coordinates. Then interpolate and expose them on the material panel.
$$
\begin{aligned}
& b: \quad R^2 \mapsto R^3, \quad \text { for } w=1-uv, \quad u, v, w \geq 0 \
& b(u, v)= \sum_{i+j+k=3} b_{ijk} \frac{3!}{i!j!k!} u^iv^jw^k \
&= b_{300} w^3+b_{030} u^3+b_{003} v^3 \
&+b_{210} 3 w^2 u+b_{120} 3 wu^2+b_{201} 3 w^2 v \
&+b_{021} 3 u^2 v+b_{102} 3 wv^2+b_{012} 3 uv^2 \
&+b_{111} 6 wuv .
\end{aligned}
$$
// Barycentric interpolation as a function
float3 BarycentricInterpolate(float3 bary, float3 a, float3 b, float3 c) {
return bary.x * a + bary.y * b + bary.z * c;
}
float3 CalculateBezierPosition(float3 bary, float smoothing, float3 bezierPoints[7],
float3 p0PositionWS, float3 p1PositionWS, float3 p2PositionWS) {
float3 flatPositionWS = BarycentricInterpolate(bary, p0PositionWS, p1PositionWS, p2PositionWS);
float3 smoothedPositionWS =
p0PositionWS * (bary.x * bary.x * bary.x) +
p1PositionWS * (bary.y * bary.y * bary.y) +
p2PositionWS * (bary.z * bary.z * bary.z) +
bezierPoints[0] * (3 * bary.x * bary.x * bary.y) +
bezierPoints[1] * (3 * bary.y * bary.y * bary.x) +
bezierPoints[2] * (3 * bary.y * bary.y * bary.z) +
bezierPoints[3] * (3 * bary.z * bary.z * bary.y) +
bezierPoints[4] * (3 * bary.z * bary.z * bary.x) +
bezierPoints[5] * (3 * bary.x * bary.x * bary.z) +
bezierPoints[6] * (6 * bary.x * bary.y * bary.z);
return lerp(flatPositionWS, smoothedPositionWS, smoothing);
}
// The domain function runs once per vertex in the final, tessellated mesh
// Use it to reposition vertices and prepare for the fragment stage
[domain("tri")] // Signal we're inputting triangles
Interpolators Domain(
TessellationFactors factors, //The output of the patch constant function
OutputPatch<TessellationControlPoint, 3> patch, // The Input triangle
float3 barycentricCoordinates : SV_DomainLocation) { // The barycentric coordinates of the vertex on the triangle
Interpolators output;
...
// Calculate tessellation smoothing multipler
float smoothing = _TessellationSmoothing;
#ifdef _TESSELLATION_SMOOTHING_VCOLORS
smoothing *= BARYCENTRIC_INTERPOLATE(color.r); // Multiply by the vertex's red channel
#endif
float3 positionWS = CalculateBezierPosition(barycentricCoordinates,
smoothing, factors.bezierPoints,
patch[0].positionWS, patch[1].positionWS, patch[2].positionWS);
float3 normalWS = BARYCENTRIC_INTERPOLATE(normalWS);
float3 tangentWS = BARYCENTRIC_INTERPOLATE(tangentWS.xyz);
...
}
Compare the effects, PN triangles off and on.
4.3 Improved PN triangles – Output subdivided normals
Traditional PN triangles only change the position information of the vertices. We can combine the normal information of the vertices to output dynamically changing normal information to provide better light reflection effects.
In the original algorithm, the change of normals is very discrete. As shown in the figure below (above), the normals provided by the two vertices of the original triangle may not be able to well represent the change of the normals of the original surface. We want to achieve the effect shown in the figure below (below), so we need to use quadratic interpolation to obtain the possible surface changes in a single patch.
Since the surface is a cubic Bezier surface, the normal should be a quadratic Bezier surface interpolation, so three additional normal control points are required.TheTusThe article has been explained clearly. Please go to the detailed mathematical principlesRef10. Link.

The following is a brief introduction on how to obtain the normal direction of the subdivision.
First, get the two normal information of point AB. Then find their average normal.

Construct a plane perpendicular to line segment AB and passing through its midpoint.

Take the reflection vector of the average normal just taken for the plane.

Count each side, so there are three.

struct TessellationFactors {
float edge[3] : SV_TessFactor;
float inside : SV_InsideTessFactor;
float3 bezierPoints[10] : BEZIERPOS;
};
float3 CalculateBezierControlNormal(float3 p0PositionWS, float3 aNormalWS, float3 p1PositionWS, float3 bNormalWS) {
float3 d = p1PositionWS - p0PositionWS;
float v = 2 * dot(d, aNormalWS + bNormalWS) / dot(d, d);
return normalize(aNormalWS + bNormalWS - v * d);
}
void CalculateBezierNormalPoints(inout float3 bezierPoints[10],
float3 p0PositionWS, float3 p0NormalWS, float3 p1PositionWS, float3 p1NormalWS, float3 p2PositionWS, float3 p2NormalWS) {
bezierPoints[7] = CalculateBezierControlNormal(p0PositionWS, p0NormalWS, p1PositionWS, p1NormalWS);
bezierPoints[8] = CalculateBezierControlNormal(p1PositionWS, p1NormalWS, p2PositionWS, p2NormalWS);
bezierPoints[9] = CalculateBezierControlNormal(p2PositionWS, p2NormalWS, p0PositionWS, p0NormalWS);
}
// The patch constant function runs once per triangle, or "patch"
// It runs in parallel to the hull function
TessellationFactors PatchConstantFunction(
InputPatch<TessellationControlPoint, 3> patch) {
...
TessellationFactors f = (TessellationFactors)0;
// Check if this patch should be culled (it is out of view)
if (ShouldClipPatch(...)) {
..
} else {
...
CalculateBezierControlPoints(f.bezierPoints,
patch[0].positionWS, patch[0].normalWS, patch[1].positionWS,
patch[1].normalWS, patch[2].positionWS, patch[2].normalWS);
CalculateBezierNormalPoints(f.bezierPoints,
patch[0].positionWS, patch[0].normalWS, patch[1].positionWS,
patch[1].normalWS, patch[2].positionWS, patch[2].normalWS);
}
return f;
}And it should be noted that all interpolated normal vectors need to be standardized.
float3 CalculateBezierNormal(float3 bary, float3 bezierPoints[10],
float3 p0NormalWS, float3 p1NormalWS, float3 p2NormalWS) {
return p0NormalWS * (bary.x * bary.x) +
p1NormalWS * (bary.y * bary.y) +
p2NormalWS * (bary.z * bary.z) +
bezierPoints[7] * (2 * bary.x * bary.y) +
bezierPoints[8] * (2 * bary.y * bary.z) +
bezierPoints[9] * (2 * bary.z * bary.x);
}
float3 CalculateBezierNormalWithSmoothFactor(float3 bary, float smoothing, float3 bezierPoints[10],
float3 p0NormalWS, float3 p1NormalWS, float3 p2NormalWS) {
float3 flatNormalWS = BarycentricInterpolate(bary, p0NormalWS, p1NormalWS, p2NormalWS);
float3 smoothedNormalWS = CalculateBezierNormal(bary, bezierPoints, p0NormalWS, p1NormalWS, p2NormalWS);
return normalize(lerp(flatNormalWS, smoothedNormalWS, smoothing));
}
// The domain function runs once per vertex in the final, tessellated mesh
// Use it to reposition vertices and prepare for the fragment stage
[domain("tri")] // Signal we're inputting triangles
Interpolators Domain(
TessellationFactors factors, //The output of the patch constant function
OutputPatch<TessellationControlPoint, 3> patch, // The Input triangle
float3 barycentricCoordinates : SV_DomainLocation) { // The barycentric coordinates of the vertex on the triangle
Interpolators output;
...
// Calculate tessellation smoothing multipler
float smoothing = _TessellationSmoothing;
float3 positionWS = CalculateBezierPosition(barycentricCoordinates, smoothing, factors.bezierPoints, patch[0].positionWS, patch[1].positionWS, patch[2].positionWS);
float3 normalWS = CalculateBezierNormalWithSmoothFactor(
barycentricCoordinates, smoothing, factors.bezierPoints,
patch[0].normalWS, patch[1].normalWS, patch[2].normalWS);
float3 tangentWS = BARYCENTRIC_INTERPOLATE(tangentWS.xyz);
...
}There is another problem that needs to be noted. When we use the interpolated normal, the tangent vector corresponding to it is no longer orthogonal to the interpolated normal vector. In order to maintain orthogonality, a new tangent vector needs to be calculated.
void CalculateBezierNormalAndTangent(
float3 bary, float smoothing, float3 bezierPoints[10],
float3 p0NormalWS, float3 p0TangentWS,
float3 p1NormalWS, float3 p1TangentWS,
float3 p2NormalWS, float3 p2TangentWS,
out float3 normalWS, out float3 tangentWS) {
float3 flatNormalWS = BarycentricInterpolate(bary, p0NormalWS, p1NormalWS, p2NormalWS);
float3 smoothedNormalWS = CalculateBezierNormal(bary, bezierPoints, p0NormalWS, p1NormalWS, p2NormalWS);
normalWS = normalize(lerp(flatNormalWS, smoothedNormalWS, smoothing));
float3 flatTangentWS = BarycentricInterpolate(bary, p0TangentWS, p1TangentWS, p2TangentWS);
float3 flatBitangentWS = cross(flatNormalWS, flatTangentWS);
tangentWS = normalize(cross(flatBitangentWS, normalWS));
}
[domain("tri")] // Signal we're inputting triangles
Interpolators Domain(
TessellationFactors factors, //The output of the patch constant function
OutputPatch<TessellationControlPoint, 3> patch, // The Input triangle
float3 barycentricCoordinates : SV_DomainLocation) { // The barycentric coordinates of the vertex on the triangle
...
float3 normalWS, tangentWS;
CalculateBezierNormalAndTangent(
barycentricCoordinates, smoothing, factors.bezierPoints,
patch[0].normalWS, patch[0].tangentWS.xyz,
patch[1].normalWS, patch[1].tangentWS.xyz,
patch[2].normalWS, patch[2].tangentWS.xyz,
normalWS, tangentWS);
...
}
References
- https://www.youtube.com/watch?v=63ufydgBcIk
- https://nedmakesgames.medium.com/mastering-tessellation-shaders-and-their-many-uses-in-unity-9caeb760150e
- https://zhuanlan.zhihu.com/p/148247621
- https://zhuanlan.zhihu.com/p/124235713
- https://zhuanlan.zhihu.com/p/141099616
- https://zhuanlan.zhihu.com/p/42550699
- https://en.wikipedia.org/wiki/Barycentric_coordinate_system
- https://zhuanlan.zhihu.com/p/359999755
- https://zhuanlan.zhihu.com/p/629364817
- https://zhuanlan.zhihu.com/p/629202115
- https://perso.telecom-paristech.fr/boubek/papers/PhongTessellation/PhongTessellation.pdf
- http://alex.vlachos.com/graphics/CurvedPNTriangles.pdf