Nonstandard FDTD 笔记 前言

该笔记分为初级、中级和高级三个部分。

初级篇主要介绍一维的标准和非标准 FDTD 理论。

中级篇会介绍二维 FDTD 理论。其中二维的 NS-FDTD 理论通过组合不同的有限差分模型来提高求解 Maxwell 方程的精度，是该方法的核心之一。

高级篇会介绍三维 FDTD 理论，将其应用到导电介质（例如金属、等离子体等）中，以研究电磁波在这些材料中的传播特性。

NS-FDTD 算法的优势

有限差分时域法（FDTD） 是计算电磁波传播最著名的数值算法之一。FDTD 方法可以模拟任意形状的结构、非线性介质，并且能够计算宽频带电磁波的传播。NS-FDTD 通过对单一频率波计算的优化减少了计算资源，使得在相同资源消耗的情况下可以计算更高精度的结构。利用 NS-FDTD 方法，研究者们已经成功准确模拟了一类特殊的电磁模式——耳语回廊模式（Whispering Gallery Modes, WGM）。

耳语回廊模式指的是电磁波或声波在一个圆形、球形或环形结构的内壁附近传播，并在其周围绕行多次而不易散射到外部的现象。

一个直观的例子是，在伦敦圣保罗大教堂的圆形穹顶下，如果一个人在一侧轻声耳语，另一个人在远离数十米的另一侧仍然可以听到。这是因为声音波沿着圆形墙壁传播，并保持在特定的路径上，从而减少了能量损失。

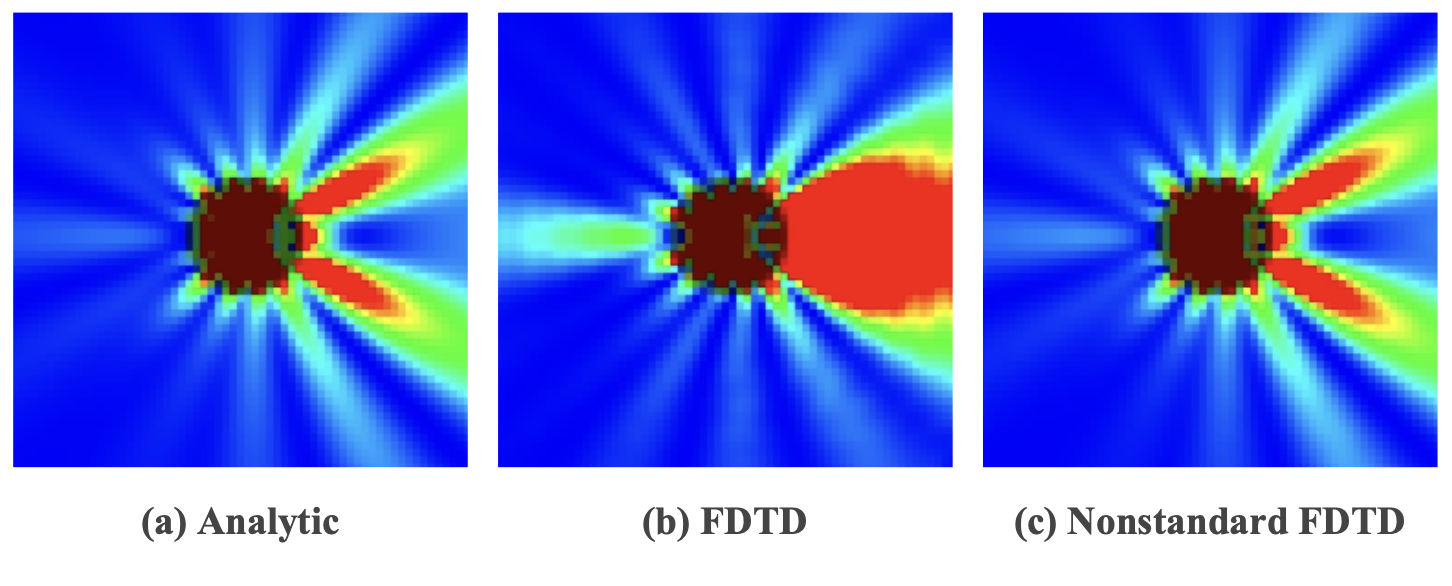
传统的 FDTD 方法在计算 WGM 的时候往往误差较大，但是NS-FDTD 方法精度更高，因此计算结果更接近于理论值，如上图所示。

(a) 图：Mie 理论的解析解，作为参考标准。

(b) 图：使用 传统 FDTD 方法在粗网格上进行的模拟，结果与理论值偏差较大。

(c) 图：使用 NS-FDTD 方法在相同粗网格上的模拟，结果与 Mie 理论 高度吻合，明显优于传统 FDTD 计算结果。

初级篇

首先介绍一维的标准/非标准 FDTD 理论。在计算机模拟中，需要额外考虑的是数值稳定和边界条件。

1. 有限差分模型（Finite Difference Model）

很多偏微分方程（PDEs）没有解析解，因此只能依赖数值模拟。有限差分（FDM）是最常见的数值计算方法，基本思想是用差分表达式来近似求解微分方程。

1.1 前向差分（Forward Finite Difference, FFD）

求解一个一维函数的导数，首先使用泰勒展开（Taylor Series Expansion），对函数 $f(x)$ 在 $x+\Delta x$ 处的展开：
$$f(x + \Delta x) = f(x) + \Delta x \frac{df(x)}{dx} + \frac{\Delta x^2}{2!} \frac{d^2 f(x)}{dx^2} + \cdots , \tag{1}$$
当 $\Delta x$ 足够小的时候，可以忽略高阶项（即 $\frac{\Delta x^2}{2!} \frac{d^2 f(x)}{dx^2} + \cdots$ ），只保留第一阶导数项，最后整理可以得到：
$$\frac{df(x)}{dx} \approx \frac{f(x+\Delta x) – f(x)}{\Delta x} . \tag{2}$$
公式（2）称为前向有限差分（Forward Finite Difference, FFD）近似。

在泰勒展开中忽略了 $\frac{\Delta x^2}{2!} \frac{d^2 f(x)}{dx^2} + \cdots$ 这一项，因此截断误差为一阶误差，即 $O(\Delta x)$ 。

1.2 后向差分（Backward Finite Difference, BFD）

类似地，对函数 $f(x)$ 在 $x – \Delta x$ 处的展开：
$$f(x – \Delta x) = f(x) – \Delta x \frac{df(x)}{dx} + \frac{\Delta x^2}{2!} \frac{d^2 f(x)}{dx^2} + \cdots . \tag{3}$$
易得：
$$\frac{df(x)}{dx} \approx \frac{f(x) – f(x- \Delta x)}{\Delta x} . \tag{4}$$
误差同上。

1.3 中心差分（Central Finite Difference, CFD）

前面两个算法都只用了当前点与一个相邻点计算，因此精度较低。中心差分则是使用前后两个相邻点，提高了精度。

对于函数 $f(x)$ ，将公式（1）与公式（3）相减，消去二阶导数项，得到：
$$f(x + \Delta x) – f(x – \Delta x) = 2\Delta x \frac{df}{dx} + O(\Delta x^3) . \tag{5}$$
进一步整理得到：
$$\frac{df}{dx} \approx \frac{f(x + \Delta x) – f(x – \Delta x)}{2\Delta x} . \tag{6}$$
有些教材会用 $\Delta x/2$ 替换 $\Delta x$ 得到公式（7），两者其实是等价的。
$$\frac{df}{dx} \approx \frac{f(x + \Delta x/2) – f(x – \Delta x/2)}{\Delta x} . \tag{7}$$
上面两个公式都被称为二阶中心有限差分（central finite difference）公式。

另外，对于函数 $f(x)$ ，将公式（1）与公式（3）相加，消去一阶导数项后得到：
$$f(x+ \Delta) + f(x- \Delta) = 2f(x) + \Delta x^2 \frac{d^2 f}{dx^2} + O(\Delta x^4). \tag{8}$$
整理后得到：
$$\frac{d^2 f}{dx^2} \approx \frac{f(x + \Delta x) – 2f(x) + f(x – \Delta x)}{\Delta x^2} \tag{9}$$

1.4 高阶有限差分（Higher-Order Finite Difference）

在有限差分法中，通过增加采样点数的方法提高计算精度进而得到更高阶的差分公式。

为了提高精度，这里在二阶中心有限差分法的基础上额外增加两个采样点 $x + 2\Delta x, x – 2\Delta x$ ，并在此处进行泰勒展开：

对于右侧点，泰勒展开为：
$$f(x+2\Delta x) = f(x) + 2\Delta x\frac{df(x)}{dx} + 2\Delta x^2 \frac{d^2f(x)}{dx^2}+O(\Delta x^3) , \tag{10}$$
类似地，
$$f(x – 2\Delta x) = f(x) – 2\Delta x \frac{df(x)}{dx} + 2\Delta x^2 \frac{d^2 f(x)}{dx^2} + O(\Delta x^3) . \tag{11}$$
通过线性组合（比如将公式（11）取反再取半，上面两式相加），消除高阶误差项，得到：
$$\frac{d^2 f(x)}{dx^2} \approx \frac{1}{\Delta x^2} \left[ \frac{4}{3} (f(x + \Delta x) + f(x – \Delta x)) – \frac{1}{12} (f(x + 2\Delta x) + f(x – 2\Delta x)) – \frac{5}{2} f(x) + \cdots \right] . \tag{12}$$
这个模型使用了四个点，并且通过加权平均减少了误差。但是会带来数值不稳定等潜在问题。

当我们用高阶有限差分来取代微分方程时，会引入额外的数值解，即虚假解（spurious solutions）。这些解实际并不存在，是由于高阶差分方程的离散化特性导致的。

比如一阶微分方程如 $\frac{df}{dx} = f(x)$ 通常有一个独立解，二阶微分方程如波动方程 $\frac{d^2f}{dx^2}=k^2f(x)$ 通常会有两个独立解（两个自由参数），四阶微分方程会有四个独立解等等。

在数值计算中，若使用四阶有限差分方法来近似一个原本为二阶的微分方程，那么差分方程的结束就会强行提高了，进而导致额外的虚假解。这些多出来的解并不对应原本的物理系统。

尤其是描述电磁波传播的二阶微分波动方程，应该使用二阶中心有限差分法，而不是更高阶的方法。

2. 一维波动方程

在计算机上模拟波的传播，需要用到数值方法近似计算。其中，有限差分时域法则发挥强大的作用。

一维波动方程的数学表达为：
$$\frac{\partial^2 \psi}{\partial t^2} = v^2 \frac{\partial^2 \psi}{\partial x^2} , \tag{1}$$
其中 $\psi(x,t)$ 表示波的振幅， $v$ 是波的传播速度（光在真空中是 $3 \times 10^8$ 米/秒）。

这个方程的物理意义是：波的变化与时间、空间变化有关。

对于一个无限长的波动介质，解通常是一个形式非常简单的行波：
$$\psi(x,t) = A \cos(kx – \omega t) + B \sin(kx – \omega t) . \tag{2}$$
这种情况适用于自由空间传播的电磁波。比如固定边界，行波可以用正弦函数展开：
$$\psi(x,t) = \sum_{n} A_n \sin(k_n x) \cos(\omega_n t). \tag{3}$$
但是如果边界不规则，例如电磁波在地面上反射、水波冲击海岸线、声波在多个房间传播等情景，则无法简单地展开成正弦或者指数的形式，解析求解将极其复杂。比如声波接触不同介质的墙面会有不同的反射路径，导致声波的传播路径变得无法直接求解。

解析解通常会假设波速 $v$ 是恒定的，也就是波在均匀介质中传播。但是实际上波会穿过非均匀介质，如声波在不同温度的房间具有不同的传播速度。在这些情况下，波动方程会变成变系数偏微分方程，如：
$$\frac{\partial^2 \psi}{\partial t^2} = v(x)^2 \frac{\partial^2 \psi}{\partial x^2} , \tag{4}$$
其中速度 $v$ 会随着位置 $x$ 变化，导致无法直接使用傅立叶变换求出解析值。

又或者是波动方程右侧有激励源，即多个波形都有可能不同的源相互干涉，这种情况也很难求出解析解。

并且在真实世界中，能量的传播会有损耗，因此需要对波动方程引入损耗项，此时波动方程就会变成非线性方程或者高阶微分方程，使得无法直接求解。

因此我们引入有限差分时域法来解决这些问题。

2.1 标准 FDTD 算法

由于计算机不能直接计算连续的数学方程，因此需要离散化，即将空间与时间划分为网格，然后让计算机逐步计算每个格子的波动情况。

在连续的形式下，一维波动方程
$$\frac{\partial^2 \psi}{\partial t^2} = v^2 \frac{\partial^2 \psi}{\partial x^2} , \tag{1*}$$
的等价形式是
$$\left( \frac{\partial^2}{\partial t^2} – v^2 \frac{\partial^2}{\partial x^2} \right) \psi(x,t) = 0. \tag{5}$$
因此，用间隔 $\Delta x$ 离散空间，每个点用索引 $i$ 来表示 $x = i\Delta x$ ；用间隔 $\Delta t$ 离散时间，每个时刻用缩影 $n$ 来表示 $t = n\Delta t$ ，其中 $n$ 均为整数。所以把波函数写为：
$$\psi_i^n = \psi(i\Delta x, n\Delta t) . \tag{6}$$
然后用中心有限差分（central finite difference）方法计算波函数的微分。

时间与空间方向的二阶偏导函数的中心有限差分近似分别是
$$\frac{\partial^2 \psi}{\partial t^2} \approx \frac{\psi_i^{n+1} – 2\psi_i^n + \psi_i^{n-1}}{\Delta t^2} , \tag{7}$$

$$\frac{\partial^2 \psi}{\partial x^2} \approx \frac{\psi_{i+1}^{n} – 2\psi_i^n + \psi_{i-1}^{n}}{\Delta x^2} . \tag{8}$$

其中 $\psi_{i+1}^{n}$ 是右侧相邻网格点的波动值。

将公式（7）和公式（8）代入波动方程（公式（1）），得到公式（9）。
$$\frac{\psi_i^{n+1} – 2\psi_i^n + \psi_i^{n-1}}{\Delta t^2} = v^2 \frac{\psi_{i+1}^{n} – 2\psi_i^n + \psi_{i-1}^{n}}{\Delta x^2} , \tag{9}$$
整理后便得到标准的1D FDTD计算公式，1D standard finite difference time domain (FDTD) algorithm：
$$\psi_i^{n+1} = 2\psi_i^n – \psi_i^{n-1} + \left( \frac{v^2 \Delta t^2}{\Delta x^2} \right) (\psi_{i+1}^{n} – 2\psi_i^n + \psi_{i-1}^{n}) . \tag{10}$$
这个公式的依赖时间、空间中前后两个步进点计算的。也就是说当前点的状态收到相邻点的影响。

2.2 非标准 FDTD 算法

在标准 FDTD 方法中，使用中心差分近似离散波动方程。但是这个方法存在数值色散（numerical dispersion）问题。在较粗网格的时候会有很大的误差。

非标准 FDTD 算法则解决了上述问题。NS-FDTD 对单色波做特别处理，即使数值离散也能确保精度。

首先假设我们研究的是某种单色波
$$\psi(x,t) \;=\; e^{\,i(kx – \omega t)}, \tag{11}$$
其中 $k$ 为波数（$k = 2\pi / \lambda$）， $\omega$ 为角频率（$\omega = 2\pi f$）。

公式（11）连续情况下的空间微分是
$$\frac{\partial \psi}{\partial x} \;=\; i\,k\, \psi(x,t). \tag{12}$$
举个例子，如果直接用标准差分来算 $\Delta_x \psi(x,t)$ ，会得到
$$\Delta_x \psi(x,t) = \psi(x+\Delta x,t) – \psi(x,t) = e^{\,i(kx – \omega t)}\bigl(e^{\,i\,k\,\Delta x} – 1\bigr) , \tag{13}$$
和真实的微分并不一致。只有当 $\Delta x$ 足够小时，才能近似。也就是说，如果网格较粗，那么就会产生所谓的误差。

NS-FDTD 引入修正因子 $s(\Delta x)$ 让离散的算符尽可能减少误差
$$\Delta_x \psi(x,t) \approx s(\Delta x)\,\frac{\partial \psi(x,t)}{\partial x}. \tag{14}$$
这个 $s(\Delta x)$ 由 $\Delta x$ 处的相位变化量决定。例如，我们的目标是
$$\Delta_x \psi(x,t) = \psi(x+\Delta x,t) – \psi(x,t) . \tag{15}$$
那么误差因子的大小由公式（12）（13）（14）（15）共同推导出
$$
s(\Delta x)

=\frac{\Delta_x \psi(x,t)}{\partial_x \psi(x,t)}

\frac{e^{\,i\,k\,\Delta x} – 1}{i\,k\,\Delta x}

\times \Delta x

\frac{e^{ik\Delta x} – 1}{ik}.
\tag{16}
$$通过欧拉公式，将误差因子简化为$$
s(\Delta x)
= \frac{2}{k}\,\sin!\Bigl(\frac{k\,\Delta x}{2}\Bigr)\,e^{\,i\,\frac{k\,\Delta x}{2}} .
\tag{17}
$$
注意到，当 $\Delta x \to 0$ 时，非标准差分就退化回“标准中心差分”的情形，与真正的导数近似几乎一致。其实，公式（17）包含了相位因子和幅度两个部分，前者对应指数部分。

类似地，推导出时间方向的修正函数
$$s(\Delta t) = \frac{2}{\omega}\,\sin\Bigl(\frac{\omega\,\Delta t}{2}\Bigr)e^{-\,i\omega\,\Delta t/2}. \tag{18}$$
总结一下，我们从波动方程开始，将空间和时间的离散化之后用中心差分近似，然后引入修正函数（关于修正函数的指数项其实被隐含地处理了）
$$\frac{\psi_i^{n+1} – 2\psi_i^n + \psi_i^{n-1}}{\left(\frac{2}{\omega} \sin(\omega \Delta t / 2)\right)^2} = v^2 \frac{\psi_{i+1}^{n} – 2\psi_i^n + \psi_{i-1}^{n}}{\left(\frac{2}{k} \sin(k \Delta x / 2)\right)^2}. \tag{19}$$
整理后得到
$$\psi_i^{n+1} = -\psi_i^{n-1} + \left(2 + u_{\text{NS}}^2 d_x^2 \right) \psi_i^n , \tag{20}$$
其中
$$u_{\text{NS}} = \frac{\sin(\omega \Delta t / 2)}{\sin(k \Delta x / 2)} . \tag{21}$$

3. 一维 FDTD 稳定性

在做数值模拟时，我们希望时间步长 $\Delta t$ 尽量大，从而减少总的计算步数，但又不能超过某个极限，否则数值解会发散。这个极限究竟是怎么推导出来的？