Written in September 2020. I wrote it for fun. I will optimize the code in the next article. It is very unprofessional QAQ.
This article starts with the study of music theory, starting from the twelve-tone equal temperament, introducing some basic and necessary music theory knowledge, and then writing a python file to output a chord audio file.
Music theory knowledge part:
1. Brief Introduction to Temperament
1. Introduction
Temperament, also known as "music", is the science that studies the composition and application of musical scales. Temperament studies the musical scales used in music. The sounds used in music are mostly fixed, while the musical scale is based on a certainintervalA system of musical tones based on the law of pitch and specified by mathematical methods. Each unit in the system is called a "law"; a musical scale is a series of tones composed of several laws selected from the law system according to certain specifications of interval relationships, and each unit in it is called a "tone". When "tone" and "law" are collectively referred to as "musical law", in addition to the law system, it also refers to all musical tones with precise specifications.
In short, the law is to use mathematical methods to determine the vibration frequency of each pitch (not just one). "Law" is the basic unit of the law system. The concepts of "law" and "sound" are similar but slightly different. Each unit in the law system is called a "law", while each unit in the scale is called a "sound". The relationship between the law system and the scale is very close.
2. Calculation of Laws
Temperament calculation method is the interval calculation method, which uses frequency ratio or interval value to represent and calculate the size of the interval.
From ancient times to the present, laws have been constantly changing. Different legal systems are determined by different laws of life.
There are four types of interval values: logarithmic value, octave value, cent value and average interval value.
3. Circle-of-fifths system
The fifth generation law stipulates that the frequencies of the two notes that form a perfect fifth interval are set at 2:3. This method of generating a law every fifth degree and continuing to generate each law is called the "fifth generation method".

Among them, due to the existence of the maximum tone difference, the fifth-generation law cannot be circulated on the twelve-tone scale to form the scale of each key. That is, starting from the tonic, after generating the law twelve times (or more times) and incorporating it into the same octave, it is impossible to return to the tonic. This creates certain obstacles to the use of the fifth-generation law.

4. Just intonation
The frequencies of the notes in the scale are derived from ratios of small integers. In this system, the intervals between notes are based on simple numerical ratios, such as 2:1 for an octave, 3:2 for a perfect fifth, and 4:3 for a perfect fourth. These ratios create harmonically pure intervals that are said to produce more natural and pleasing to the ear than the isothermal tuning system used in modern Western music.
5. Twelve-tone equal temperament
The twelve-tone equal temperament is a tuning system that divides an octave into twelve semitones with equal frequency ratios, also known as the "twelve-equally proportional temperament".
All of our codes below are based on the twelve-tone equal temperament. The reason is that the piano is designed based on the twelve-tone equal temperament.
Baidu Encyclopedia writes: The twelve-tone equal temperament was first proposed by a scientist in the Ming Dynasty of my country.Zhu ZaiyuDiscovered in 1584. Later spread to the West via the Silk Road.
1605 Dutch mathematicianSimon SteffenIn an unfinished manuscript "Van de Spiegheling der singconst" it was proposed to use
He calculated the twelve-tone equal temperament, but due to insufficient precision, the string length figures he calculated deviated from the correct number by as much as one or two units.
The frequency ratio of an octave is 2:1, so the frequency ratio between the various tones of the twelve equal temperaments should be:
In music practice, musicians at that time were well aware of the convenience of the twelve-tone equal temperament. Composers and performers from all over the world began to use the twelve-tone equal temperament and were also committed to its development. For example, JS Bach of Germany wrote two volumes of "Well-Tempered Piano Music". Although these two volumes did not only use the twelve-tone equal temperament (some irregular temperaments were also used), they are considered to be exemplary works that fully utilized the effectiveness of the twelve-tone equal temperament and could be freely transposed.
6. Comparison of the three systems
Each of the three tuning systems has its own advantages and disadvantages. The twelve-tone equal temperament solves some contradictions between the fifth-tone temperament and the pure temperament, such as the contradiction that the starting temperament cannot be returned to after increasing the number of temperaments, but the twelve-tone equal temperament will affect the harmony of the interval. In general, the twelve-tone equal temperament reconciles and compromises the fifth-tone temperament and the pure temperament, which is between the two and closer to the fifth-tone temperament. The twelve-tone equal temperament is currently the most widely used tuning system.
2. Basic Music Theory - P1 - Musical Tone System and Grouping
1. Music system and musical series

There are 88 keys on a piano. The sum of these musical notes is called –Music System.
Arranged from low to high is called –Tone Series.
2. Note name
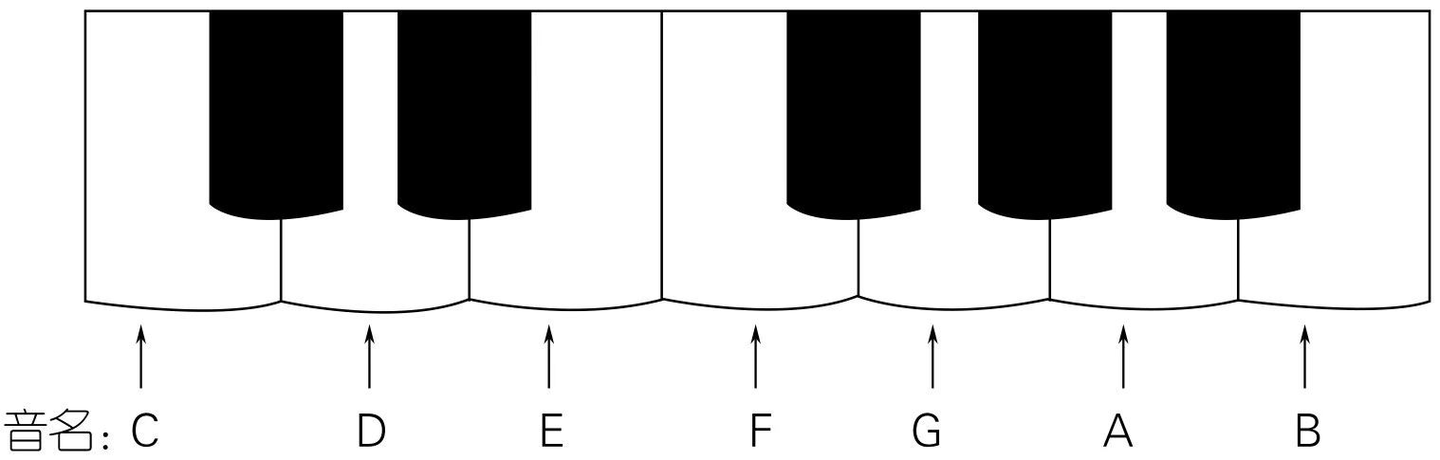
In the musical system, each musical note has a fixed name, i.e., note name, which is usually represented by letters C, D, E, F, G, A, B.
These seven pitches are also called basic pitches, and their positions on the piano keyboard are fixed.

3. Sound grouping
The piano is divided into different areas.

The group of notes starting from the middle C on the piano keyboard is called the small note group 1, also known as the "axis group". The small note group 1 to the right is called the small note group 2, small note group 3, small note group 4, and small note group 5; the small note group 1 to the left is called the small note group, large note group, large note group 1, and large note group 2.

3. Basic Music Theory - P2 - Staff & Notes
1. Staff
The staff is composed of five lines and four spaces, which are used to record the pitch of notes. Because the staff has five equidistant parallel horizontal lines, it is called the five-line staff.

2. Clef
Here we just need to briefly introduce the treble clef. In addition, there are also bass clef and alto clef.


3. Musical Notes
A note consists of three parts: the note head (the hollow or filled oval symbol), the stem (the short vertical line), and the tail (the small arc on the right side of the stem).

4. Rest
Rests are symbols used to indicate pauses or interruptions in music.
During the progress of music, although the rest indicates a brief silence, it has a special meaning at this time, and the music is not interrupted, so the rest is one of the important components of a musical work.

5. Time Signature
The numerator number represents the number of beats in a measure, and the denominator number represents how many notes make up a beat. Be careful not to read it as a fraction of a beat!
In addition, the time signature also clarifies the rules for changes in the strength of the melody.

4. Basic Music Theory - P3 - Intervals
1. Interval
The pitch distance between two notes is called the interval.
There are two types of intervals: melodic intervals and harmonic intervals.
In short, a melodic interval is when two notes sound one after the other, while a harmonic interval is when they sound at the same time.
2. Melodic intervals
Read in the order of pronunciation.

3. Harmonic Intervals
The lower note is called the root note, and the upper note is called the crown note.


4. Consonant and dissonant intervals
The sound effects of consonant intervals sound pleasant and harmonious, and can be divided into perfect consonant intervals and incomplete consonant intervals.
Perfect consonant intervals include perfect first, perfect fourth, perfect fifth, and perfect octave; imperfect consonant intervals include minor third, major third, minor sixth, and major sixth.
The sound of pure octave sounds very integrated, like the sound of one note, but because it is too integrated, the sound will sound hollow.
The sound effects of the perfect first, perfect fourth, and perfect fifth intervals are slightly fuller than those of the perfect octave, but they also appear hollow.
Therefore, all pure intervals (perfect first, perfect fourth, perfect fifth, perfect octave) are perfectly consonant intervals.
The sound of dissonant intervals is harsh, tense and unstable, such as major and minor seconds, major and minor sevenths, augmented fourths and diminished fifths.
Although dissonant intervals sound sharp, they are also important elements in musical works.
5. Basic Music Theory - P4 - Mode
1. Tuning
A system of musical notes of different pitches, organized around a stable central tone (tonic) in a certain relationship, is called a mode. The most widely used mode in the world today is the major and minor mode.
Among them, Bach's "Well-Tempered Clavier" is a classic among classics in major and minor keys.

2. Tonic
In the mode, the tonic is the central tone in the core position, which has the strongest sense of stability and other tones tend to it. In songs (music), the tonic often appears on the strong beat, the longer tone or the ending.
3. Major Mode
The major scale is abbreviated as "major" and consists of seven scales. The major third is the interval between the tonic and the Ⅲ scale, which is also the characteristic of the major scale. Among them, the Ⅰ, Ⅲ, and Ⅴ scales form a major triad, so the color of the major scale is bright and brilliant.

There are three types of major keys: natural major, harmonic major, and melodic major.
1. Natural major
The natural major is the most commonly used major key, consisting entirely of natural notes.

The natural major scale consists of five whole tones and two half tones.
Its scale structure is: whole tone-whole tone-semitone-whole tone-whole tone-whole tone-semitone, that is, it is composed of major second, major second, minor second, major second, major second, major second, and minor second intervals.

There is a tone (black key) between C and D, so the CD is called full tone.
There is no interval between E and F, so it is called a semitone.
To make it easier to memorize, the natural major key is compiled into a mnemonic: full, full, half, full, full, full, half.
That is what we usually say: de re mi fa sol la si
The key of C natural major is shown below:

2. Harmonic major
On the basis of the natural major scale, lowering the VI note by a semitone results in the harmonic major scale.
Its characteristic is the augmented second interval formed between the flat VI and VII notes.
This augmented second is the mark of the harmonic major key and also the characteristic of the harmonic major key.
The C harmonic major scale is shown below:

3. Melodic major
On the basis of the natural major scale, lowering the VI note by a semitone results in the melodic major scale.
Its characteristic is the augmented second interval formed between the flat VI and VII notes.
This augmented second is the mark of the harmonic major key and also the characteristic of the harmonic major key.
The C melodic major scale is shown below:

4. Minor mode
The minor mode is simply called "minor" and is also composed of seven pitches.
The relationship between its tonic and the Ⅲ degree is a minor third, which is also the characteristic of the minor mode. Among them, the Ⅰ, Ⅲ, and Ⅴ degrees form a minor triad, so the color of the minor mode is soft and dim.

There are also three types of minor keys: natural minor, harmonic minor, and melodic minor.
1. Natural minor
The natural minor scale also consists of five whole tones and two semitones, and its scale structure is whole tone-semitone-whole tone-whole tone-semitone-whole tone-whole tone, that is, it is composed of major second, minor second, major second, major second, minor second, major second, and major second intervals.
The a natural minor scale is shown below:

To make it easier to memorize, the mnemonic is: whole, half, whole, whole, half, whole, whole.

2. Harmonic minor
On the basis of the natural minor scale, raising the seventh degree by a semitone results in the harmonic minor scale.
Its characteristic is the augmented second interval formed between the VI and the raised VII, and the VII has the function of a leading tone tending towards the tonic after being raised by a semitone, and it is more tense than the natural minor.
The a harmonic minor scale is shown below:

3. Melodic minor
On the basis of the natural minor scale, the VI and VII degrees in the ascending scale of the natural minor are raised by a semitone, and then these two notes are restored in the descending scale, which is the melodic minor.
The a-melodic minor scale is shown below:

6. Basic Music Theory—P5—Key Signature
1. Key Signature
The key signature is a symbol that indicates the pitch (i.e. the pitch of the main note) of a song (music). It is located at the beginning of each line of the staff (after the clef) or where a new key appears during the music.
Key signatures are written using sharp and flat signs.






Python arrangement part:
1. Understanding the MIDO library
1. Import mido
from mido import Message,MidiFile,MidiTrack
2. Mido basic framework
Create two mido library objects: MidiFile(), MidiTrack()
The former is used to edit, generate and output Midi files, and the latter is used for midi file track editing.
mid = MidiFile() track = MidiTrack() mid.tracks.append(track)
Add information in track object, 'program_change' means switch track.
The intuitive understanding is: before editing a track, you need to select the track first. (This is the official fixed routine, it doesn’t matter if you don’t understand it, just follow it)
track.append(Message('program_change', program=0, time=0))3. Write notes
After selecting the track, you can add notes directly to the track. Note that the time unit here is milliseconds.
track.append(Message('note_on', note=60, velocity=64, time=0))After adding, add an end mark, and this is the point where the writing of a note is truly completed.
track.append(Message('note_off', note=60, velocity=64, time=2000))After adding, you can directly generate a midi file
mid.save('MyFirstDamnSong.mid')4. Code
The code is as follows:

2. Combined with Music Theory
1. Midi file frequency number table:

From the table above, we can see that the midi number of middle C is 60.
2. Writing tool library
1. Task Analysis
We first write a tool library Notes_Toolbox.py to define some commonly used and basic things.
Define the basics: intervals, note names, modes, chords, beats, fundamental notes, etc.
Then write some simple methods for calling, such as returning a set of chords, automatically changing the key, and getting the MIDI frequency number through the five-line score.
2. Define variables
| serial number | Variable Name | Is static? | Default value | effect |
| 1 | bpm | No | 125 | Beat |
| 2 | timePerBeat | No | 60 / bpm * 100 | Duration of each beat (milliseconds) |
| 3 | base_note | static | 60 | MIDI number for middle C |
| 4 | note_name[] | static | ['C','D','E','F','G','A','B'] | musical alphabet |
| 5 | major_notes[] | static | [0, 2, 2, 1, 2, 2, 2, 1] | Diatonic Scale |
| 6 | Cmajor_notes[] | static | ||
| 7 | Eflatmajor_notes[] | static | ||
| 8 | Cmajor{} | static | {'C': 60, 'D': 62, 'E': 64, 'F': 65, 'G': 67, 'A': 69, 'B': 71} | C major dictionary |
| 9 | Eflatmajor{} | static | {'C': 63, 'D': 65, 'E': 67, 'F': 68, 'G': 70, 'A': 72, 'B': 74} | E minor dictionary |
| … | … | … | … | … |
3. Define functions
| serial number | Method Name | return | Passing in parameters | effect |
| 1 | get_note | MIDI Number | note,group=0,**kw | Enter the note name and note area, and return the corresponding MIDI number. (Needs improvement, no black keys) |
| 2 | get_chord | Chord Array | name, **kw | Enter the chord name and return the chord array |
| 3 | originToEflatMajor | New E minor MIDI number array | list,**kw | Enter C major and return E minor. (Needs improvement to support specifying which key to change to) |
| … | … | … | … | … |
bpm = 125 #why 125: #bpm = 1 * 1000 / 8 timePerBeat = 60 / bpm * 1000 base_note = 60 # C4 note_name =[ 'C','D','E','F','G','A ','B' ] major_notes = [0, 2, 2, 1, 2, 2, 2, 1] Cmajor_notes = [] Eflatmajor_notes = [] for num in range(12): Cmajor_notes.append(base_note+sum(major_notes[0:num+1])) Eflatmajor_notes.append(base_note+ 3+sum(major_notes[0:num+1])) # There is only one area Cmajor = dict(zip(note_name,Cmajor_notes)) # Cmajor = {'C':60,'D':62,'E':64,'F':65,'G':67,'A':69,' B':71} Eflatmajor = dict(zip(note_name,Eflatmajor_notes)) # Eflatmajor = {'C': 63, 'D': 65, 'E': 67, 'F': 68, 'G': 70, 'A': 72, 'B': 74} def get_note(note,group=0,**kw ):#Group = 0 means 4Group global base_note,major_notes return base_note + group*12 + sum(major_notes[0,note]) def originToEflatMajor(list,**kw): Ef=[] for x in list: Ef.append(x+3) return Ef #get_note(1,group=0) return 60 #get_note(2,group=0) return 62 def get_chord (name): chord = { "Major3":[0,4,7,12],# Major triad "Minor3":[0,3,7,12],# Minor triad "Augmented3":[0,4,8,12],# Augmented triad "Diminished3":[0,3,6,12],# Diminished triad "M7":[0,4,7,11],# Major seventh chord "Mm7":[0,4,7, 10],#dominant seventh chord "m7":[0,3,7,10],#minor seventh chord "mM7":[], #... } return chord[name] #get_chord("Major") return [ 0,4,7,12]3. Write a chord breakdown
Now that we have written the tool module, we can focus on the chord part.
1. Write an output chord function
Output broken chords to midi files
When using this method, you need to pass in:
| serial number | Parameter name: | Incoming: | Example: |
| 1 | track | Output audio interface of mido library | MidiTrack() |
| 2 | root | The name of the note | 'C','D','E','F','G','A','B' |
| 3 | name | The name of the chord, defined in Notes_Toolbox | 'Major 3'… |
| 4 | format | Outputting the broken chords | [0,1,2] [1,3,2,3]… |
| 5 | length | How long the note lasts | 4 |
Just put the source code:
def add_broken_chord(root, name, format, length, track, tone_name='Cmajor', root_base=0, channel=0): # The default is C major root_num = Notes_Toolbox.Cmajor if tone_name == 'Eflat': root_num = {'C': 63, 'D': 65, 'E': 67, 'F': 68, 'G': 70, 'A': 72, 'B': 74} root_note = root_num[root] + root_base*12 # 解作根音time = (length * 480) / len(format) # This is the official document writing, I don’t understand it either. Time refers to the duration of the note for broken_chord in format: # Through the for loop, output the notes of the chord one by one note = root_note + Notes_Toolbox.get_chord(name)[broken_chord] track.append(Message('note_on', note=note, velocity=60, time=0, channel=channel)) track.append(Message('note_on', note=note, velocity=60, time=round(time), channel=channel))2. Call reference:
format = [0, 1, 2, 3] add_broken_chord('C', 'Major3', format, 4, track) add_broken_chord('C', 'Minor3', format, 4, track) add_broken_chord('C', ' Augmented3', format, 4, track) add_broken_chord('C', 'Diminished3', format, 4, track) add_broken_chord('C', 'Diminished3', format, 4, track)Finally, call to save the midi file.
3. Standardized Code
In order to facilitate calling, we adjust the order of function parameters.
In addition, overload the play_note method so that it can receive the int type note (that is, directly input the MIDI number).
Similarly, all note-related inputs can be overloaded.
def play_note(note, track, length=1, tone_name='Cmajor', root_base=0, delay=0, velocity=1.0, channel=0): ... def play_note(note:int, track, length=1, tone_name='Cmajor', root_base=0, delay=0, velocity=1.0, channel=0): ... def play_broken_chord(root, name, format, track,length=1, tone_name='Cmajor', delay=0, velocity=1.0,root_base=0, channel=0): ...
4. Conclusion: Mido journey is yet to be continued…
After the above learning and practice, I have a simple understanding of the connection between music and mathematics, and some basic music theory knowledge. Through the code, the output of various chords is realized.
Combining music theory knowledge, next, we will write circle chords.
References
.Basics of Music Theory”, edited by Li Chongguang, People’s Music Publishing House;
Leave a Reply